알고리즘을 작전별로 보자!
Greedy AlgorMinimum - Spanning Treeithms
답을 찾기 위해 선택을 반복하는 알고리즘 중 비교적(?) 간단한 방법으로 선택하고 선택한 후 바꾸지 않는 알고리즘
<그래프>

그리디 작전을 쓴다면 가장 짧은 쪽으로 계속 간다. B>A>C>D...?? 지금은 안된다. 물론 풀리는 예도 있다.
<선택정렬>

selection sort도 그리디였다.
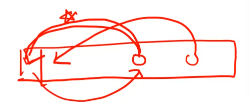
가장 작은 걸 앞으로 보낸다. 뒤돌아보지 않는다!
<Minimum Spanning Tree>
undirect graph에서 Minimum Spanning을 정의할 수 있다.

node가 5개, edge 4개 고르면 tree가 된다.
(node n개인 tree는 edge가 n-1개)
Tree: Connected Acyclic Graph
모든 노드가 연결되어 있고 사이클이 없는 그래프
간단한 증명

degree가 1인 노드가 있다는 것을 알 수 있다.
degree가 전부 2이상이라고 하면(degree가 1인 노드가 없다면)
항상 다른 edge를 통해 나갈 수 있다. => 사이클을 만들 수 있다.
사이클이 없어야 하므로 degree가 1인 노드가 있어야 한다.

n=k인 트리가 있다면 거기에서 degree가 1인 노드와 엣지를 빼버리면 노드가 k-1개인 트리가 된다.
=> connected가 깨지지 않는다.
=> acyclic도 깨지지 않는다.
<Prim Algorithm>
추가할 수 있는 edge 중 가중치가 가장 작은 것을 추가한다.
인간이 이해할 수 있게 표현한 주장 (증명 아님)
- 아무 하나의 노드를 가진 트리에서 시작 (하나의 노드가 곧 트리라고 생각)
- 트리에 인접한 에지들 중 가장 작은 웨이트를 가진 에지를 추가 (단, 사이클을 만들지 x)
- spanning tree가 될 때까지 반복

s에서 시작한 예 => 이 예제에서는 답을 찾는다.
1. 정확성
그리디가 정확하다는 것을 증명하는 방법은 standard한 방법이 있다.
답이 여러개 있는 경우에 증명이 어렵다.
edge weight가 같은 것이 없다고 생각하고 증명을 하기도 한다.
(여기서는 같은 게 있을 수 있다고 생각하겠다. 더 일반적인 증명이고 더 많은 걸 알 수 있다)
답이 여러개 있을 수 있는 데 그 중에 하나를 Tmst라고 하겠다.
정답 중 아무거나 하나를 잡고 증명을 시작하는 것!
prim알고리즘이 돌아가는 과정을 보며 증명하겠다. (직관적으로 증명x)
Tmst를 벗어나느냐 안 벗어나느냐를 보는 것.
1, 노드 하나를 선택한다. (당연히 벗어나지 않는다.)
2. weight가 가장 작은 edge 하나를 선택한다.
이 때까지는 Tmst를 벗어나지 않았다.
같은 과정 반복 중 ... 정답에 없는걸 고르면?

즉, prim 알고리즘이 edge weight가 가장 작아서 e1을 골랐다면?
prim 알고리즘이 Tmst는 안만든다.
하지만 정답은 여러개이며 프림 알고리즘은 다른 정답을 만들고 있다.
다른 정답과 비교하여 모순이 아니다. 라는 것을 계속 보이면 된다. => 이것이 작전!!
Tmst U {e1} 이란 Tmst에 e1을 추가한 집합 => 추가한 엣지를 포함하는 사이클이 한개가 생긴다. e1 a1 a2 a3 a4 ......
이 사이클 안에 이번 라운드에서 고려대상이었던 다른 edge가 있다 -> e2
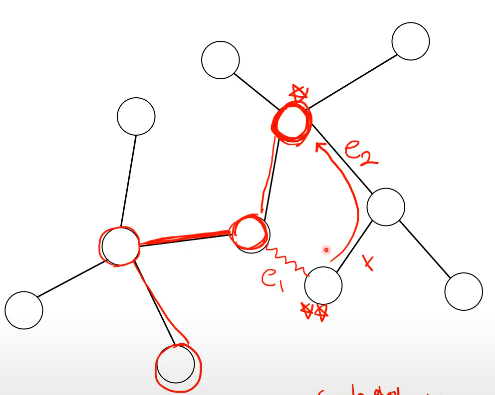
☆☆과 x는 기존 트리에 들어있지 않았다.
e1을 포함하지 않는 사이클을 돌면 반드시 트리에 들어 있던 노드를 만나게 된다. = ☆노드
트리에 포함된 것(☆)과 포함되지 않은 것을 연결 (e2) => 항상 e2를 찾을 수 있다.
e1과 e2의 웨이트를 비교
1. w(e1) > w(e2) => e1을 고를 이유가 없다. e1을 고르지 않았을 것 (모순)
2. w(e1) < w(e2) => (Tmst - {e2}) U e1 => Tmst가 정답이라는 것에 모순 (정답보다 작은 답이 있다?)
3. w(e1) = w(e2) => (Tmst - {e2}) U e1 = Tmst' 얘도 정답이다! (하나가 빠지고 weight가 같은게 하나 들어감)
정확성 증명 끝!
결국 프림 알고리즘이란 트리에 인접한 것 중에 제일 작은노드 연결을 반복하는 것이다~
2. 코드로 나타내기 (성능)
어떻게 실제 코드로 바꾸고, 빠르게 동작시킬 수 있을까?
다시 돌아와서,
- 아무 하나의 노드를 가진 트리에서 시작 (하나의 노드가 곧 트리라고 생각)
- 트리에 인접한 에지들 중 가장 작은 웨이트를 가진 에지를 추가 (단, 사이클을 만들지 x)
- spanning tree가 될 때까지 반복
트리에 들어갔냐 안들어갔냐는 노드마다 표시를 하면 된다.

0을 다 넣어놓고 2에서 시작 => 1로 바꿔준다.
e1 = (a,b)
이때 a와 b는 하나는 0, 하나는 1이어야 한다! 둘다 1,1이면 사이클을 만들게 된다.
모든 엣지를 살펴보면서 1,0인걸 고른다. 각각에는 weight가 붙어있을 텐데 가장 낮은 걸 고른다.
이경우
node n개
edge m개 있는데
n-1번의 라운드를 돌면서 m개를 계속 보겠지. => O(mn) 너무 느리다.
O(m+n)수준이 되어야 빨리 돌아간다고 할 수 있다.
코드와 거의 비슷한 스타일로 써두었다. 그렇다면 각각을 어떻게 코드로 바꿀 것인가?

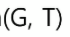
G = 입력 그래프
T = 출력 (edge set. 실제로는 배열)

ex)
입력 = 인접 리스트
출력 = (1,3,5) / (1,5,8) : 노드 번호 2개와 weight임 = 엣지 하나


엣지를 출력하는 배열임.
엣지 n-1개를 넣을 것인데 현재 몇 개가 들어가있는지 카운트 변수만 가지고 있으면 된다.

시작할 때 1번노드에만 마킹 되어 있다라는 뜻
While U!=V
T의 edge 개수 < n-1

갯수로 판단할 수 있음 n-1이 되면 끝

u = U에 이미 들어있던 노드
v = U에 들어있지 않던 노드
= 마킹 된 노드와 마킹되지 않은 노드를 잇는 엣지 중 웨이트가 가장 작은 것을 찾는다.
=> priority Queue (Heap)을 쓰면 된다
찾고 나면,

= edge set에 하나 추가한다.

= 0에서 1 마킹만 하면 된다.
구현 시작

1번 노드에 연결된 4개의 edge를 모두
priority Queue에 넣는다.

여기서 하나를 꺼내면 weight가 가장 작은 것이 나올 것이다.
= (a,b,w)
a,b의 마킹이 하나는 0, 하나는 1인지 봐야 한다.
(첫단계라서 둘다 11일수는 없지만 둘다 1이라면 이 edge는 버린다. 사이클이 되기 때문에)
0,1 또는 1,0이라면 이 엣지를 선택한다. (인접한 엣지 중 weight가 가장 작다는 뜻)

선택하면 노드가 하나 추가되겠지
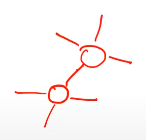
마찬가지로 새로 추가된 노드에 붙어있는 엣지를 다 집어 넣는다.

역시 weight가 가장 작은 애가 나올 것
꺼낼 때 1,1이 아닌지 체크한다.


이미 있는 엣지가 또 추가되어도 상관없음(들어갈때 체크할 필요가 없다는 뜻)
집어넣을 때 체크해도 나올때 1,1로 달라질 수 있기 때문에
라운드마다 시간이 다르지만
모든 엣지가 몇번 들어가는지 생각해보자.
2번씩 들어갔다가 나온다. (공유되는 엣지)
엣지 하나가 들어갔다 나오는 시간은 log m
모든 엣지가 들어갔다 나왔다 = 2mlogm
= O(mlog m)
모든 노드에 한번씩 마킹
전체 시간 = O(n+mlog m)
O(n+mlog n)이라고 쓰기도 함.... m이 아무리 커봤자 n^2
또, m이 더 크므로 n을 생략하고 O(mlog m이라고 해도 되지만!)
'알고리즘' 카테고리의 다른 글
| 알고리즘6 Djikstra Algorithm (0) | 2020.09.17 |
|---|---|
| 알고리즘5 - Kruskal Algorithm (0) | 2020.09.16 |
| 알고리즘3-2 자료구조 리뷰2 (0) | 2020.09.10 |
| 알고리즘3 자료구조 리뷰 (0) | 2020.09.10 |
| 알고리즘2-2 재귀적 선택 정렬 , 합병정렬 , 퀵소트 (0) | 2020.09.06 |



