내 프로그램이 정확하다는 말은 언제든지 할 수 있어야 한다.
Prim알고리즘은 한 노드에서 시작해서 퍼져 나간다.
엣지를 추가한다는 점에서 유사하다.
Kruskal Algorithm는 전체 그래프에서 가장 작은 엣지를 추가한다.

1,2,3을 추가한 상태이고 이제 4를 추가해야 하지만 두 개의 4 모두 추가하면 사이클이 된다. PASS

프림 알고리즘에서는 이미 들어간 노드와 안들어간 노드를 연결하면 사이클이 생기지 않았다.
Kruskal 에서는 어떻게 사이클을 판단할 것인가?
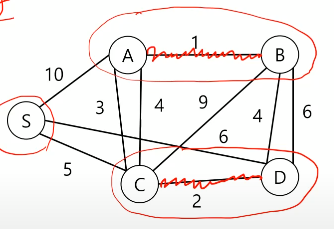
같은 덩어리를 연결하면 사이클이 생긴다. 연결이 안된 노드는 하나의 덩어리라고 생각
이러면 답을 찾느냐? 성능은 어떻게 되는가?
정확성
프림 알고리즘과 마찬가지로 정답은 여러개일 수 있다. 정답 중 하나를 찾는다는 것을 증명한다.
하지만 특정한 답을 잡고 증명시작하는 것이 더 쉽다.
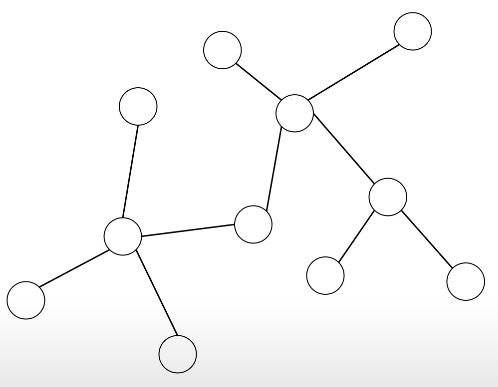
저 그림은 하나의 정답이 아니지만 저 정답과 모순이 없다면 정답을 잘 찾고있는 것

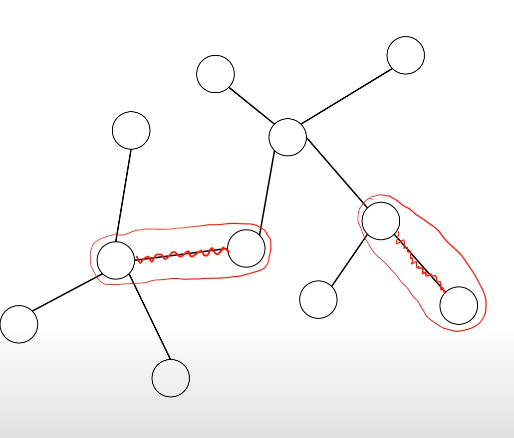
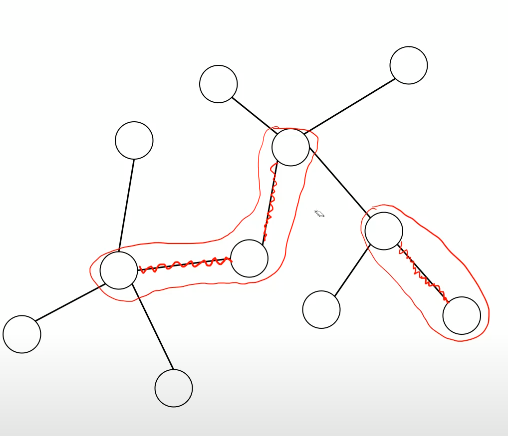
지금 총 덩어리는 8개 (하나인 노드 포함!)
Tmst 정답에 없는 것을 추가했을 때

정해진 정답과 다르게 연결했지만 여전히 이것이 정답임을 보이면 된다.
Tmst = 정답 엣지 집합
Tmst U {e} => 사이클 있음 (e포함)

e와 연결된 두 개의 노드를 따라 쭉 따라가면 돌아오는 것을 생각할 수 있다. (사이클 있음)
이 사이클에 e말고, Tmst에 있지만 알고리즘이 아직 추가하지 않은 edge가 있다.
알고리즘에 이미 추가한 엣지도 있고, 아직 추가하지 않은 엣지도 있다.
다시 말하면,
생성된 사이클에 아직 추가하지 않은 edge가 반드시 있을 것이다.
(같은 덩어리에 있는 것끼리는 추가할 수 없으니까.)
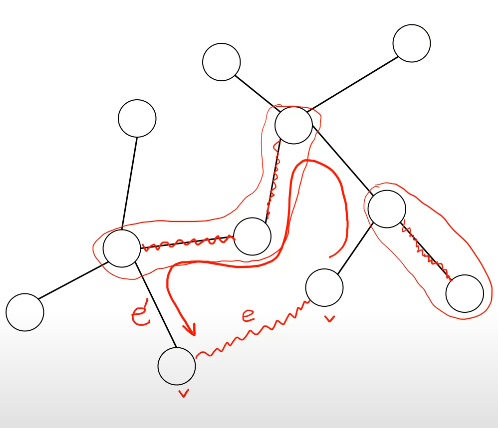
사이클 안에서 추가되지 않은 엣지 중 하나를 e'이라고 하자.
(e'는 서로 다른 덩어리를 연결하고 있음
1. e'가 같은 덩어리를 연결했다면 정답안에 사이클이 있다는 뜻
2.e를 연결하고 있는 노드와 노드는 서로 다른 덩어리일테니까)
이렇게 세 가지 경우가 있겠지
1. w(e) > w(e') => 알고리즘의 모순이다. 가장 작은 엣지부터 추가한다고 했으니까!
2. w(e) < w(e') => Tmst - {e'} U {e} -> Tmst보다 더 좋은 정답
3. w(e) = w(e') => Tmst - {e'} U {e} -> Tmst보다 더 좋은 정답
구현 및 성능

가장 작은 가중치는 배열에서 순서대로 보면되고
사이클이 있는지 없는지만 체크하면 된다. Union Find로 거의 상수 시간
sorting은 당연히 O(mlog m)
전체: O(mlog m)

앞에 부터보면서 추가할 것인가 말것인가 보면 된다.
(a,b,w)
a,b가 같은 덩어리에 있는지 아닌지를 판단해야 한다.
=>DFS
O(n+m) , m이 작기 떄문에 O(n)이라 생각해도 될듯
월등히 더 빠른 방법은
Union Find (덩어리 합치기)
덩어리마다 대장 노드가 생긴다. 특정 노드에서 find를 하면 대장의 번호가 나온다.
Find(a) -> 대장 번호
Find(b) -> 대장 번호
같은 번호면 같은 덩어리, 다른 번호면 다른 덩어리
다른 덩어리라서 두개를 이으면 대장 하나는 죽는다!

노드마다 덩어리가 트리로 되어 있다. 노드들은 전부 parent를 가르킨다.
대장은 루트이며, 어느 노드든 루트까지 올라가면 대장을 찾는다.

트리 형태마다 속도가 다르겠지만 find에 적합하게 링크를 고치는 Path Compression 사용해 성능 향상
'알고리즘' 카테고리의 다른 글
| 알고리즘7 다익스트라, BFS (0) | 2020.09.23 |
|---|---|
| 알고리즘6 Djikstra Algorithm (0) | 2020.09.17 |
| 알고리즘4 Greedy Algorithms - Prim Algorithm (0) | 2020.09.10 |
| 알고리즘3-2 자료구조 리뷰2 (0) | 2020.09.10 |
| 알고리즘3 자료구조 리뷰 (0) | 2020.09.10 |



