재귀적 선택 정렬

loop보다 살짝 더 느리다.
이해하기는 더 쉽다.
전체를 살펴보고 제일 작은 숫자를 찾는다.
첫번째 값과 제일 작은 숫자를 바꾼다.
제일 작은 숫자를 빼고 나머지를 sorting하면 전체가 sorting되는 것
그래서 그 뒤의 배열을 재귀적으로 보내준다.
재귀이므로 sorting이 잘된다고 믿으면 된다.
proof by induction


n-1일때는 재귀 호출이기 때문에 그냥 믿는다.
n일때 a[0] < a[1]만 성립한다고 보이면 된다.
a[0]는 무엇인가?
재귀 호출하기 전에 제일 작은 값
a[0] < a[x] if x>0
a[1]은 무엇인가?
원래 a[1]~a[n-1] 중 한 값이 a[1]일 것이다. (집합조건은 안 깨지기 때문에)
우리가 알 수 있는 사실은
a[1]이 뭐였든 간에 a[1]은 a[x]중 하나이며
a[0]는 a[x]보다 작은 값이기 때문에 항상 a[1]보다는 작은 값이다.
재귀적 선택 정렬 시간 복잡도

T(n) = n + T(n-1) 은 사실이다.
식을 풀어나가다보면 n + n-1 + n-2 + n-3 + ... + 2 + 1
Merge Algorithm
시간: O(n)
단점: 배열이 하나 더 필요하다. merge를 한 공간에서 못한다.
배열 만들고 복사하는 데에 시간이 더 소요된다.

두 배열에서 꺼내어 더 작은 값을 결과 배열에 옮긴다. x 반복

집합 조건이 없어지는 코드는 없다.
쪼개지고 합쳐지더라도 재귀적으로 집합 조건이 안 깨진다고 믿는다.
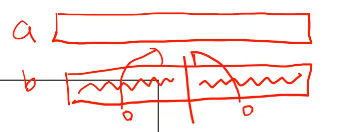
a배열을 통째로 b로 옮겨서 복사하고
b를 반으로 나누어 왼쪽sorting 오른쪽sorting해서 다시 a에 합친다.
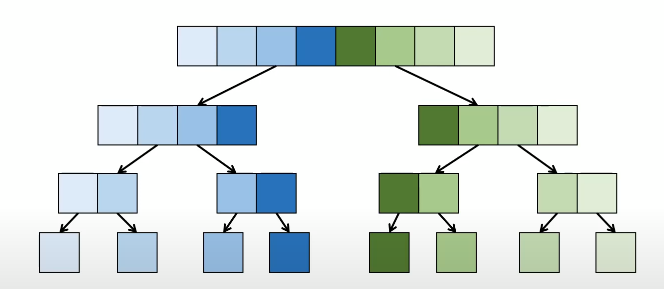
재귀함수를 잘 보는 법은 밑에까지 따라 내려가지 않고
한단계만 보는 것...!
Merge Algorithm 시간 복잡도

절반으로 나누고 합치고...O(n)
절반짜리 재귀호출이 2개 2T(n/2)
log n번 내려가면 T(1)=1 or 0이 되어 계산이 끝난다.
분모 분자 곱하면 계속 n이 나온다.
=> nlog n
선택정렬 : O(n^2)
합병정렬 : O(nlogn)
(일반적인 sorting은) nlog n 보다 빠른 sorting은 없다.
Quick Sort
추가 배열을 안 만들기 위한 정렬

p=a[0]으로 시작
p가 d번째 자리로 어디론가 간다.
d-1까지는 p보다 작고, d+1부터는 p보다 크다.
(p는 자기 자리를 찾아갔다. 앞뒤로 재귀를 실행하면 된다.)

=> O(n)
Proof of Induction

재귀호출에서 집합 조건을 깨지 않는다면 나도 깨지 않는다.

이건 그냥 믿는다.

p를 기준으로 앞뒤는 재귀에서 온다. 믿으면 된다.
결국 a[d-1] < a[d]와 a[d] < a[d+1] 만 성립하면 된다.
=> 재귀 호출 전에 성립했던 내용이다.
시간 복잡도 (나중에)
퀵소트는 왼쪽 오른쪽 크기를 알 수 없다.

'알고리즘' 카테고리의 다른 글
| 알고리즘3-2 자료구조 리뷰2 (0) | 2020.09.10 |
|---|---|
| 알고리즘3 자료구조 리뷰 (0) | 2020.09.10 |
| 알고리즘2 선택 정렬 증명 (0) | 2020.09.06 |
| 알고리즘1-2 수학적 귀납법과 재귀 (0) | 2020.09.01 |
| 알고리즘1 The HALTING Problem (0) | 2020.09.01 |



