728x90
남들보다 좋은 코드를 짜기 위해선 남들이 왜 이런 코드를 짰는지 알아야 한다.
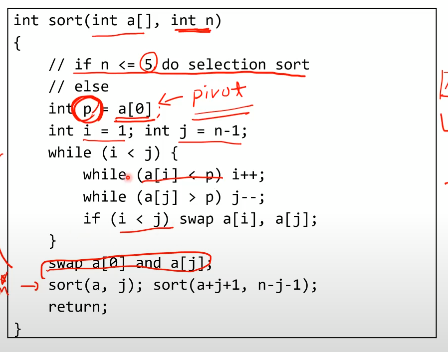

pivot의 왼쪽과 오른쪽이 비슷하면 n log n을 보장할 수 있지만
전혀 예상할 수 없는 상태이다.

Q(n): n개를 퀵소트로 정렬하는 시간이라고 하자.
Worst Case:

pivot이 한 쪽 끝에 있는 경우
Q(n) = n + Q(n-1) => Q(n) = O(n^2)
어느경우에도 worst case는 피할 수 없다(너무 긴 얘기)
Best Case:

반으로 잘라지는 경우
Q(n) = n + 2Q(n/2) => Q(n) = O(n log n)
Average Case: 모든 가능한 경우가 동일한 확률로 들어온다.
현재 compansion model이므로 비교만하면 된다.
1, 3, 2 / 2, 7, 4 => 같다.
1, 2, 3, ..., n => n! 가지
a[0] -> i등일 확률 => 1/n
내가 잡은 pivot이 1등일 확률 = 2등일 확률 = 3등일 확률 ...


왼쪽에 i-1 개, 오른쪽에 n-i 개
1부터 n까지 나오고, 나올 확률은 1/n
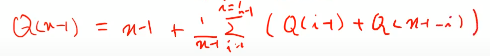

1번 식에 x n
2번 식에 x (n-1) 하면

1번식-2번식

정리하면

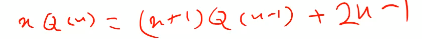
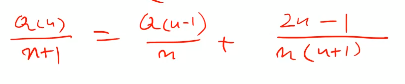


이 결과가 대충 log n이다.

Conclusion About Quicksort?

최악의 경우가 O(n^2) => 평균을 보니 직관적으로 자주 나오지 않을 것
최선의 경우가 O(nlog n)
평균의 경우가 O(nlog n)
메모리 할당을 안함으로써 넣는 성능이 크기 때문에 머지소트보다 퀵소트를 많이 쓴다.
하지만 worst case를 아예 없앨 수 없는가?
'알고리즘' 카테고리의 다른 글
| 알고리즘12 Plane Sweeping (0) | 2020.10.13 |
|---|---|
| 알고리즘 11 (0) | 2020.10.07 |
| 알고리즘9 (0) | 2020.10.02 |
| 알고리즘8 Deadline Scheduling (0) | 2020.09.27 |
| 알고리즘7-2 BFS (0) | 2020.09.23 |



