한 단계 한 단계에 집중을 하자.

a와 b의 공통 조상 중 제일 낮은 것 = LCA
노드 번호 2개를 주고 LCA x를 찾아라.
느린 방법: 각각 루트까지 올라간다.
a에서 루트까지 타고 올라간 번호와
b에서 루트까지 타고 올라간 번호 중 겹치는 가장 낮은 번호

최악의 경우가 있을 수 있으므로 O(n)
하나의 트리에서 여러 경우를 찾아야 하는 경우가 많으므로 사실상 오래걸림

a에서 DFS에서 b를 찾는 방법도 있음 (또다른 느린 방법)


1,2,4,8...위의 노드를 기억한다.
모든 노드는 O(log n)개의 값을 가지고 있게 된다.
노드는 n개이므로 계산해야하는 값의 갯수는 O(nlog n)
i는 모든 노드에 대해서 다 수행한다.
A[i][0]는 한칸 위 이므로 parent임, root인 경우 -1로 표시하면 됨 => 다 채울 수 있다.
0이 있을 때 1을 채울 수 있냐
1이 있을 때 2를 채울 수 있냐
A[i][j]까지 계산되어 있다고 치면

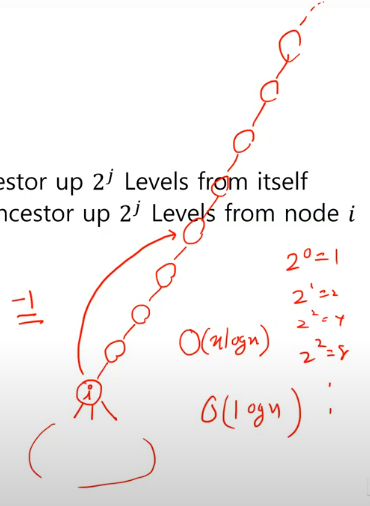
j=2, 즉 4칸 올라간 것을 알고 있을 때
j=3, 8 칸 올라간 것을 알고 싶다.
모든 노드가 j=2 (4칸) 올라간 번호를 알고 있는 상태이다.
8번 올라간 번호를 알려면
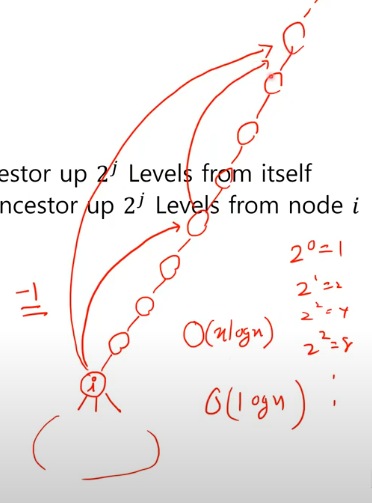
나한테서 4칸 올라간 애의 4칸 올라간 번호를 알면 된다. = 나한테서 8칸 올라간 번호임

모든 노드가 j까지 계산했으면 모든 노드가 j+1까지 계산할 수 있음
j가 log n까지 계산 가능한 것!
-1은 넣으면 안된다. 그 위는 없다는 뜻이니까
A[i][j]가 다 계산이 되었다고 치자. 여기까지 pre-processing
하나 계산하는 데에 상수시간이므로 여기까지 O(nlogn)

a와 b의 레벨이 다를 수 있다.

일단 레벨을 맞춰야 한다. 어떻게 올리는가?
두 레벨의 차이 = d
d를 이진수로 쓴다 ex) d = 00010110

4번 자리가 1이라는 것은 2^4가 있다는 것

이 숫자만큼 올라가야 한다는 뜻임

저만큼의 칸을 올라가야 한다. (올라가고 거기에서 또 올라가고 거기에서 또 올라가고)
왼쪽부터 오른쪽, 오른쪽부터 왼쪽은 상관없음

다른 노드면 분명히 그 위에 LCA가 있다.
A[a'][j] A[b][j] 인데 j를 가장 크게 놓고 본다. (j = log n = 루트까지 가겠지 = 같을 수 밖에 없다)
j를 1줄이고 같은지 본다. 같으면 계속 줄이고 본다. 다를 때까지.
최초로 다르면 여기로 jump해서 LCA를 본다.

j=3 (8칸)에서는 같았다가
j=2 (4칸)에서 최초로 달라진 것
별표 노드로 가서 LCA를 찾는데
j=2인 상태에서 왔으므로 j=2는 해볼 필요가 없고 j=1 j=0을 해보면 된다.
(별표노드에서 1칸위도 LCA가 같으므로 LCA를 찾은 것!)
'알고리즘' 카테고리의 다른 글
| 1로 만들기 (0) | 2021.02.06 |
|---|---|
| 알고리즘27 LCA (0) | 2020.12.03 |
| 알고리즘26 (0) | 2020.11.28 |
| 알고리즘25-2 Las Vegas vs Monte Carlo (1) | 2020.11.26 |
| 알고리즘25 Randomized Algorithm (0) | 2020.11.26 |

