SCC 안에서는 다른 어느 노드든 다 이동할 수 있다.

더 이상 키울 수 없는 노드들의 집합
그 안의 노드들은 양쪽으로 reachable
사이클 = SCC는 아니지만 사이클 하나는 SCC.

일단 그냥 사이클이라고 생각하고
일단 무작정 DFS를 해보자.
(cut vertex는 어디에서 시작해도 같은 결과가 나온 것과 다르게)
하지만 시작 지점에 따라 DFS tree가 다르게 나오고
전진할 수 있는 것이 여러개 있을 때 어디로 전진하느냐에 따라서 다르게 나온다.


같은 그래프지만 트리가 두개로 나올 수도!
한 트리가 여러개의 SCC를 가지고 있을 수는 있지만, 한 SCC가 여러 Tree에 나눠있지는 않다!

한 번 들어오면 다 돌기 때문에 다른 트리로 나눠질 수 없다.
한 SCC에 들어 있는 노드들이 두 개의 트리에 흩어져있다면
SCC는 두 트리끼리 이동할 수 있는 엣지가 있어야 한다. (cross 엣지)

하지만 cross링크는 한쪽으로 가능하기 때문에 모순!
먼저 간 것을 왼쪽에 그리기로 했음. 왼쪽->오른쪽으로 가는 크로스 링크는 있을 수 없음!
DFS를 돌리면 트리가 여러개 나오는데
트리는 여러개의 SCC로 구성된다.


결론: DFS를 두번 돌린다.
1. 아무 DFS를 돌리면서 post 번호를 붙인다. (떠난 순서) (cut vertex는 pre order)

2. 모든 링크를 뒤집는다. (트리가 아니라 입력 그래프에서)
3. 다시 DFS를 돌린다. 트리가 여러개 나온다면 각 트리마다 post번호가 가장 큰것에서 시작!
=> 트리하나에 SCC가 한 개씩 들어있게 된다.

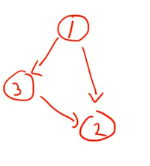
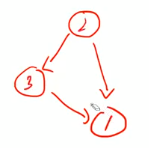
- back edge는 사이클을 만든다. => 반드시 하나의 SCC에 포함

- forward edge는 short cut => 하나의 SCC에 포함될수도/아닐수도
- cross edge는 절대로 SCC 내부의 엣지가 될 수 없다. => 절대로 하나의 SCC에 포함되지 않음


슈퍼그래프를 실제로 만들지는 않고 생각만 할 것.
(사실 SCC를 찾고나서 만들 수 있으므로 만들 수 없음)
Supergraph의 정의 :
한 SCC가 하나의 노드가 된다.

SCC와 상관없는 엣지가 있을 수 있다.
한 SCC에서 다른 SCC로 가는 링크가 하나라도 있으면 엣지 추가

슈퍼그래프는 DAG이다.
원래 그래프에서 DFS -> 슈퍼그래프에서 DFS하는 것을 생각해보면
번호가 어떻게 붙을지 생각해볼 수 있다.
<pre>
둘 다 가능하지만 어느쪽이 크다는 것이 보장되기를 원한다.
<post>

어디서 시작하든 똑같다.

이 경우에는 달라질 수 있긴 하지만
3개의 크기 관계는 항상 같다는 것이 포인트
1. 링크를 그대로 두고 post번호가 제일 작은 것에서 시작 (사이클이 없을 때만..) (안타깝지만 잘안된다.)
2. 링크를 다 뒤집고 post번호가 큰 것부터 시작
중간정리

트리와 포스트 번호를 붙였다고 하면
슈퍼그래프가 링크가 연결된 관계에 따라 번호 순서로 알 수 있어야 한다.
하지만 pre order는 잘안된다.
pre번호 자체는 한 SCC안에서도 섞여있다.
왜냐하면?


어느 것을 먼저가느냐에 따라서 번호가 섞이게 된다.
post번호도 사실은 섞여 있다..
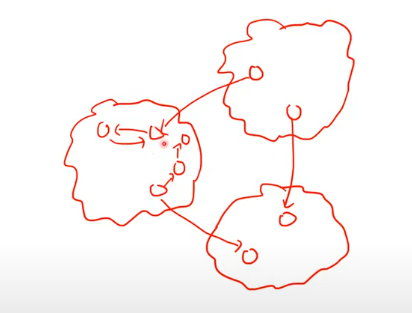
Minimum pre() (한 그룹안에서 pre번호 중 가장 작은 것) 도 섞여 있다.

슈퍼 노드를 모르는 상태에서 첫번째 dfs를 해야함..
각 SCC안의 가장 작은 노드가 다르므로 알 수 없게됨 (?)
(여기부터 다시 듣기 추천)
Maximum Post() 로 잡으면 not Mixed!!!!

한 SCC그룹에서 다른 SCC그룹으로 링크가 있으면
maximum post를 봤을 때 첫번째 DFS가 어떻게 돌더라도
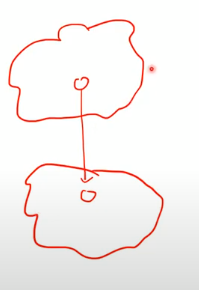
어느 그룹을 먼저 방문하든지간에 아래에서 위로 갈 수 없기 때문에
위는 아래보다 다음라운드 방문할 수 밖에 없다.
아래 그룹이 정해지고 난 후에 위에 그룹이 정해진다!
드디어 최종 알고리즘!

post num자체는 섞여 있을 수 있다.
하지만 (한 그룹에서)maximum post num을 보면 다르다!
위에서는 a나 b가 제일 크다.
전체에서 SCC를 무시하고 모든 노드의 post 번호를 보면 제일 큰 것이 a or b일 것이다.
제일 작은건 어디있는지 잘 모름
maximum중에 제일 작은건 d 아니면 e
가장 큰 것이 a라고 치자.
링크전체를 reverse 해도 SCC가 달라지지는 않는다.


a에서 시작! => a 출력
남은 부분에서 다시시작 -> 그 다음으로 큰 b에서 시작! => b 출력
남은 부분에서 다시시작 -> c에서 시작!
그 다음에 c나 f가 가장 크다는 것을 보장할 수 있다.
(d,e는 c,f보다 작으므로)
indegree가 0이 아닌 애들은 절대로 제일 클 수 없다.
indegree가 0인 애들중에 제일 큰 애들 (c,f)
결론 : 큰 번호부터 순서대로 DFS를 돌리면 된다는 것!
첫번째 DFS를 한 상황

트리들 사이에서도 말이 된다.
첫번째 dfs가 끝나고 나서 한 트리안에 SCC가 여러개있을때
post num이 큰 것부터 시작하면 된다.
(뒤집었을때 작은 것부터 시작하면 이동할 수 없는 상태이므로)
실제 SCC를 구하는 것은 슈퍼노드를 구하고 할 수 없다.
슈퍼노드의 링크만을 뒤집고 싶지만 어디까지가 슈퍼노드인지 모르기때문에 전체를 뒤집는다.
다행히 모든 링크를 뒤집어도 SCC는 유지가 된다.
SCC를 연결하는 링크만 뒤집어진다.
max post로 생각을 하면 전체에서 성립,,
'알고리즘' 카테고리의 다른 글
| 알고리즘23-2 동전 교환 (0) | 2020.11.22 |
|---|---|
| 알고리즘 23 Backtracking and Pseudopolynomial - N-Queen (0) | 2020.11.22 |
| 알고리즘21-2 (0) | 2020.11.20 |
| 알고리즘21 (0) | 2020.11.14 |
| 알고리즘20-2 Cut Vertex (0) | 2020.11.07 |



