
connected graph에서만 정의 된다. (Vertex = Node)
: 노드 s를 그래프에서 없애면 graph가 disconnect가 될 때, 그 노드를 cut vertex라고 한다.
(노드와 연결된 엣지가 없어진다.)
: 노드 x에서 노드 y로 가는 모든 path가 s를 통해서 지나가면 cut vertext라고 한다.
정의를 그대로 썼을 때의 시간,
connected Components : O(m+n)이다.
이것을 모든 노드마다 돌려야 하므로 O(n (m+n)) = O(mn+n^2)

<루트에 대해 cut certex를 확인하는 방법 2가지>
DFS tree의 루트가 cut vertex이면 child가 두 개 이상이다.
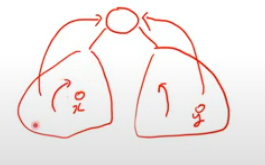
백엣지가 서브트리 안에 있으므로 서브트리를 벗어나면 무조건 루트로 오게 된다.
y는 x의 서브트리 밖에 있다. x에서 y로 가려면 루트를 거쳐야만 한다.
child가 두 개 이상이면 cut vertex이다.
=> child가 없거나 하나이면 cut vertex가 아니다.

루트를 지워도 subtree에서 연결가능

각 노드를 루트로 잡아서 DFS를 본다.
O((m+n)m) = O(mn+n^2)

모든 노드마다 l(t) 를 게산한다.
preorder 번호

루트에서 따라 위에서 아래로 내려가면 숫자가 커진다.
l(t)란? 1,2,3 중 최소
1. pre(t)
2. 나로부터 올라가는 가장 작은 back
3. 자식들의 l값 중 가장 작은 것
1+2 : 자기한테서 back edge를 타고 올라갈 수 있는 가장 높은 곳
1+2+3: t를 루트로 하는 서브트리에서 백엣지를 한 번 타고 올라갈 수 있는 가장 높은 곳
Proof
l(u) >= Pre(t)

x에서 y로 가려면 t를 지날 수 밖에 없다.
무조건 서브트리 안에 있거나 t로 오게된다.
이런 u가 하나라도 있으면 t는 cut vertex가 된다.
반대로 t가 cut vertex라면 이런 u가 있느냐? YES
이런 u가 없으면 t가 cut vertex가 아니라고 증명하면 된다.

back edge가 있다는 것은 모든 child에 대해서 위로 올라갈 수 있는 방법이 있다는 것
u와 같은 경우가 하나도 없다면 t가 cut vertex가 아닌 것이 명백하다.



