15-1 추가된 내용
전형적인 동적 프로그래밍 문제

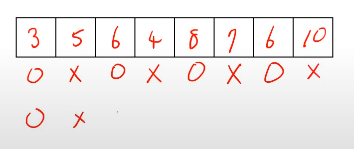
일하면 받는 돈이 써있다. 단, 연속된 날은 일할 수 없다.
마지막 날이 일할 수도, 안할 수도 있다.
마지막날에 일하는 날 중 제일 좋은 답이 있을 것이고
마지막날에 일 안하는 날 중 제일 좋은 답이 있을 것이다.
마지막 전날은 마지막 날에 영향을 받는다.

마지막 날을 제외하고 가장 좋은 답을 구하기
둘 중 하나는 제일 좋은 답일 것이다.
앞에서부터 계산해두면 뒤에서 사용할 수 있다.

인덱스0: 그 날 일을 안하는 것중에 제일 좋은 것
인덱스1: 그 날 일을 하는 것중에 제일 좋은 것
배열 생성하고 첫 날 일을 할 때&안할 때의 초기값을 넣어준다.
day2부터 계산한다.{
그 날 일을 안할 때 = MAX(그 전날 일 할때 , 그 전날 일 안할때)
그 날 일을 할 때 = 그 전날 일을 안하는 것 중에 제일 좋은 것 + 오늘 일의 효율}
max값을 리턴한다.

=>마지막 날 일하는 게 더 좋음
(실수-16이 아니라 17을 가지고 왔어야 함)
입력으로 주어진 값들에 바로 붙여서 계산하기 때문에 생각하기 살짝 편하다.

(3x2 2x4) 4x2 = 3x2
3x2x4 + 3x4x2 = 48번 계산
3x2 (2x4 4x2) = 3x2
3x2x2 + 2x4x2 = 28번 계산
결합법칙으로 어느것을 먼저 계산할지는 내맘이지만 계산 횟수가 달라진다.

Mi부터 Mj까지 행렬들을 다 곱해서 행렬하나를 만들겠다.
어떤 순서대로 곱하든 무관하기 때문에 재귀가 가능하다. => cost는 변하지 않는다.

앞에서 계산된 cost를 사용할 수 있다.
cost = Mij라고 한다면 cost는 변하지 않는다.


왼쪽꺼 만드는 비용 + 오른쪽꺼 만드는 비용 + 제일 마지막 곱하는 비용
어느것을 제일 마지막에 곱해야 하는가?

'알고리즘' 카테고리의 다른 글
| 알고리즘15-2 (0) | 2020.10.25 |
|---|---|
| 알고리즘15 (0) | 2020.10.25 |
| 14 Dynamic Programming (0) | 2020.10.17 |
| 알고리즘13 (1) | 2020.10.17 |
| 알고리즘12 Plane Sweeping (0) | 2020.10.13 |



