Convex Hull

전체가 볼록한 다각형


변의 길이가 가장 작아지고 면적도 제일 작아짐
느린 방법부터 생각해보자
N^3
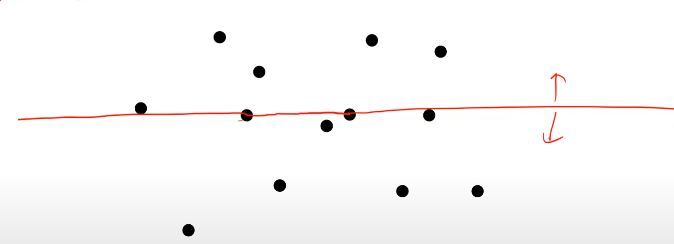
convex위에 있는 선분을 직선으로 늘린다.
모든 점이 한쪽에 다 있으면 convex위에 있는 것

모든 점이 다 한쪽에 있다! 그림으로 보면 쉬운데 코드는 어떻게 짜지..?
(설명을 편하게 하기 위한 가정)
1. 모든 X좌표는 다름
2. 모든 Y좌표도 다름
3. 한 직선 위에 3개 점이 있는 경우 없음
CCW (Counter-Clock-Wise) 시계반대방향

x좌표, y좌표가 다 다르다고 가정~
기울기로 풀려고 한다.




여기에도 이 식이 똑같이 성립한다! (좌회전)

이 변을 테스트할 것임

우회전

좌회전
다른 모든 점들에 대해서 CCW를 돌리면 좌회전도 있고 우회전도 있을 것임
= 한 직선 위에 있지 않구나~를 알 수 있다.

다른 노드들을 3번으로 CCW를 돌리면 모두 우회전
n^2 * n = O(n^3)
N^2 log n
(log n은 sorting)
Package Wrapping 각도 정렬

반직선

이 직선을 왼쪽으로 돌리며 처음 부딪히는 점을 Convex에 포함시킨다.

모든 점을 각도로 sorting하면 가장 오른쪽에 있는 애가 가장 작은 작도
double, float로 하면 오차가 있어서 순서가 바뀔 수 있다.
보통은 각도로 안하고 CCW쓴다.

어느게 왼쪽에 있고 오른쪽에 있는지 알면 sorting할 수 있다.
CCW로 하면 나누기를 안하므로 double,float계산이 아니라 정수계산!

한 변 찾는데에 nlogn쓴다.
= n * nlog n
Graham Scan
가장 가까운 점을 찾으려면 sorting해야 한다.
원점을 중심으로 하는 원위의 점들 n개


convex를 구하고 나면 각도대로 sorting한 순서가 된다.
(a다음에 b가 나온다)
3 8 2 6 5 7 9 1

전부 각도로 바꾸고, 원위에 표시
convex를 푼다 => sorting을 한다.
nlog n보다 빨리 풀수 있으면 sorting을 nlog n보다 빨리 할 수 있다는 뜻.
즉 nlog n이 가장 빠름
y좌표가 가장작은걸 고르고 각도 sorting (여기까진 앞과 같다.)
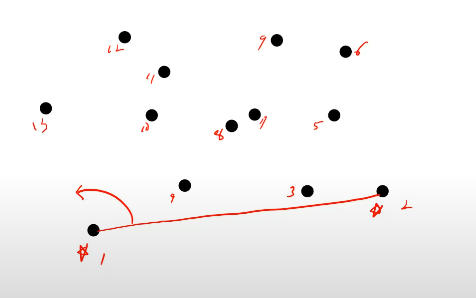
점을 그리디 비슷한 방식으로 추가할 것임. stack사용


3번 들어가면 좌회전임. (좌회전이면 점 추가)

4번 들어가도 좌회전

1,2,3 => 좌회전
2,3,4 => 좌회전

3,4,5 => 우회전
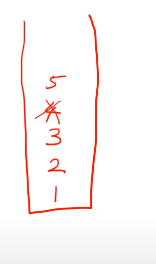
스택에서 뺀다

2,3,5 => 우회전
스택에서 또 뺀다. 좌회전이 될떄까지
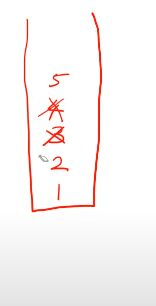


여태까지 본 점들의 convex hall이라고 할 수 있다.

1,2,X
X에는 뭐가 들어가도 좌회전이니까 2번이 스택에서 빠질일은 없다.
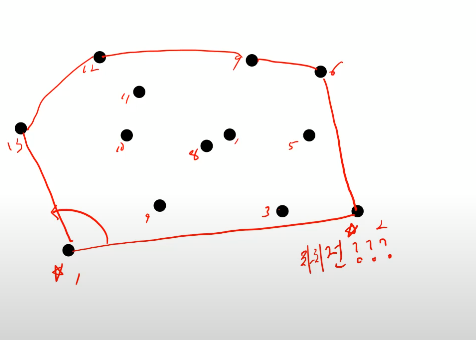
이런식으로 끝난다.
nlog n
시간이 드는건 sorting밖에 없다.
1.점 하나 잡기
2.각도 sorting
3.순서대로 보기, 좌회전이면 추가하고 아니면 빠져나오기
(모든 점은 스택에 한번들어가서 한번 나온다.)
스캔하는 시간은 O(n)